算法原理

对于一个像素$P$，它的亮度值设为$I_P$。
设定一个合适的阈值$t$。
考虑以该像素点为中心的一个半径等于3像素的离散化的Bresenham圆，这个圆的边界上有16个像素（如下图所示）。

线搜索每一次迭代首先计算搜索方向$p_k$,然后计算在这个方向上移动的 距离$a_k$。迭代式如下：

(1)$$x_{k+1}=x_k+a_kp_k$$
线搜索方法的成功依赖于能否有效选取方向$p_k$和步长$a_k$。
大多数线搜索方法需要$p_k$是下降方向，即$p_k^T \nabla f_k<0$，这个属性能够保证$f$沿着这个方向减小。搜索方向通常有如下形式：
(2)
$$
p_k =-B_k^{-1}\nabla f_k
$$
这里$B_k$是对称非奇异矩阵。在最速下降法中，$B_k$是单位矩阵。在牛顿方法中，$B_k$是Hessian矩阵$\nabla ^2 f(x_k)$。在拟牛顿方法中，$B_k$是Hessian矩阵的近似。当$P_k$定义为(2)式且$B_k$正定时，我们有：

$$
p_k^T \nabla f_k=-\nabla f^T_kb_k^{-1} \nabla f_k <0
$$

本节讨论如何选取方向和步长。

寻找最大的K个数

八大排序算法C++实现

官网如下：http://yann.lecun.com/exdb/mnist/

首页详细地介绍了数据集的二进制格式，读取非常简单，要注意的是用大端模式，还有读取的图片的方向问题。

前言

在无约束优化中，我们依赖实变量来最小化目标函数。数学表达式为：
$$\underset{x}{\text{min}}f(x)$$

其中$X \in R$ 是拥有$n \geqslant 1$个元素的实数向量，$f:\mathbb{R}^n \rightarrow \mathbb{R}$ 是光滑函数。
通常，我们对函数$f$缺乏全局的视角。我们所知道$f$的值或许只是一些它在点集$x_0,x_1,x_2,…$的导数。

题目

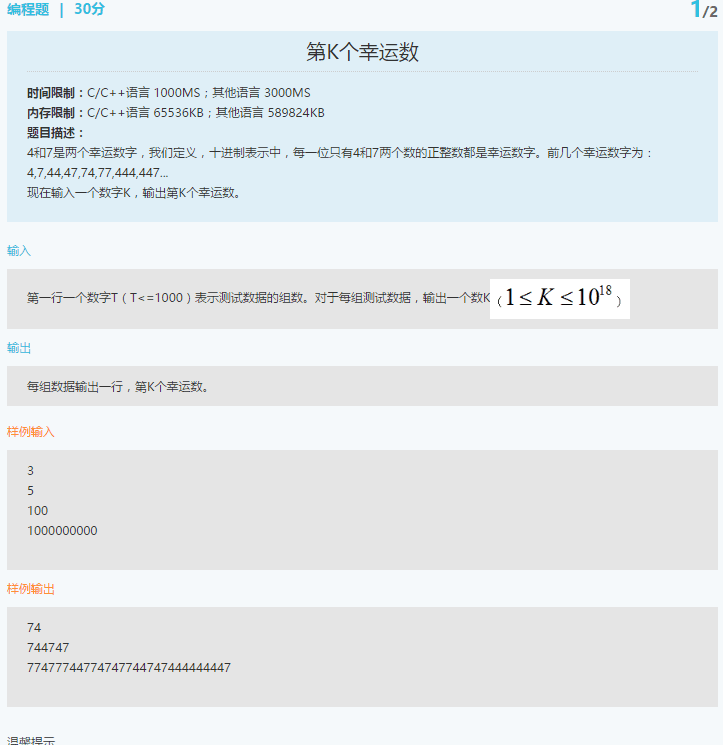
注意K的范围，程序中一定要用long long，用int达不到范围要求。
int ： -2147483648～2147483647
long long ： -9223372036854775808 ~ 9223372036854775807

数学表达

$x$ 变量集合，也叫未知参数
$f$ 目标函数
$c_i$ 约束函数，即$x$必须满足的特定等式和不等式的标量函数

使用上述定义，优化问题可以描述为
$$ \underset{x \in R^n}{\text{min}} \quad \text{subject to} \quad
\begin{array}{c}
{c_i(x)=0,\quad i \in \varepsilon ,}\\
{c_i(x) \geqslant 0,\quad i \in \tau .}\\
\end{array}
$$
这里$\varepsilon$和$\tau$分别是等式和不等式约束的下标。

描述

今天晚上做了以下滴滴的模拟题，其中有一道开关灯的问题。题意描述如下，有2015个灯，序号是1~2015，初始都是熄灭的，然后从k=1开始，序号是k的倍数灯拨一下开关，直到k=2015。问：最后亮着的灯有几盏？

Sobel算子是计算机视觉领域的一种重要处理方法。主要用于获得数字图像的一阶梯度，常见的应用和物理意义是边缘检测。在技术上，它是一个离散的一阶差分算子，用来计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子，将会产生该点对应的梯度矢量或是其法矢量。