斐波拉契加强版

题目描述

对于斐波拉契经典问题，我们都非常熟悉，通过递推公式F(n) = F(n - 1) + F(n - 2)，我们可以在线性时间内求出第n项F(n)，现在考虑斐波拉契的加强版，我们要求的项数n的范围为int范围内的非负整数，请设计一个高效算法，计算第n项F(n)。第一个斐波拉契数为F(0) = 1。
给定一个非负整数，请返回斐波拉契数列的第n项，为了防止溢出，请将结果Mod 1000000007。
测试样例：
3
返回：
2

题目解析

普通非递归解法如下：

int fib(int n) {
	if (n < 2)
		return 1;
	int cur = 1;
	int pre = 1;
	int tmp;
	for (int i = 2; i <= n; ++i)
	{
		tmp = cur;
		cur += pre;
		pre = tmp;
	}
	return cur;
}

时间复杂度O(N)。对于输入数字很大并对时间有要求时，还有更好的解法。参考《剑指offer》P75，数学公式如下。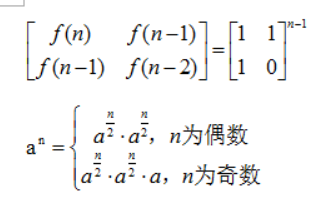

解决这个公式，可以使用快速矩阵幂，时间复杂度可减小到O(logn)。

参考答案

class Fibonacci {
	public:
	void multi(long long a[2][2], long long  b[2][2])
	{
	    long long  r[2][2];
	    r[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
	    r[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
	    r[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
	    r[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
	 
	    a[0][0] = r[0][0] % 1000000007;
	    a[0][1] = r[0][1] % 1000000007;
	    a[1][0] = r[1][0] % 1000000007;
	    a[1][1] = r[1][1] % 1000000007;
	}
	 
	int getNthNumber(int n) {
	 
	    long long  tmpA[2][2] = {
	        { 1, 1 },
	        { 1, 0 }
	    };
	    long long  tmpB[2][2] = {
	        { 1, 0 },
	        { 0, 1 }
	    };
	 
	 
	    for (; n > 1; n = n / 2)
	    {
	        if (n & 1 == 1)
	        {
	            multi(tmpB,tmpA);
	        }
	        multi(tmpA, tmpA);
	    }
	    multi(tmpA, tmpB);
	 
	    return tmpA[0][0] ;
	}
};