直线拟合之最小二乘拟合（Least Squares Fitting）和RANSAC

发表于   |   分类于   |  

直线拟合属于比较经典的优化问题了。这里探讨下使用最小二乘拟合和RANSAC两种方法进行拟合。

最小二乘拟合

直线的一般式方程：
$$ ax + by + c = 0 $$
最小二乘拟合时暂不考虑b=0的情况，考虑其斜率方程
$$y = kx + b$$
设观测样本数为N，观测误差

$$ e= \sum_{n=1}^N{(kx_i-y_i)^2} $$

为使e达到最小，分别对k，b求偏导使其等于0

$$ \frac{\partial e}{\partial k}={k\sum_{i=1}^{N}{x_i^2}}+{b\sum_{i=1}^{N}{x_i}} -{\sum_{i=1}^{N}{x_iy_i}}=0 $$

$$\frac{\partial e}{\partial b}=k\sum_{i=1}^{N}{x_i}+Nb-\sum_{i=1}^{N}{y_i}=0$$

求得

$$k=\frac{\sum_{i=1}^{N}{x_i}\sum_{i=1}^{N}{y_i}-N\sum_{i=1}^{N}{x_iy_i}}{(\sum_{i=1}^{N}{x_i})^2-N\sum_{i=1}^{N}{x_i^2})}$$

$$b=\frac{\sum_{i=1}^{N}{x_i}\sum_{i=1}^{N}{x_iy_i}-\sum_{i=1}^{N}{y_i}\sum_{i=1}^{N}{x_i^2}}{(\sum_{i=1}^{N}{x_i})^2-N\sum_{i=1}^{N}{x_i^2})}$$

RANSAC

RANSAC算法的输入是一组观测数据（往往含有较大的噪声或无效点），一个用于解释观测数据的参数化模型以及一些可信的参数。RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：

  1. 有一个模型适应于假设的局内点，即所有的未知参数都能从假设的局内点计算得出。
  2. 用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点。
  3. 如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
  4. 然后，用所有假设的局内点去重新估计模型（譬如使用最小二乘法），因为它仅仅被初始的假设局内点估计过。
  5. 最后，通过估计局内点与模型的错误率来评估模型。
    上述过程被重复执行固定的次数，每次产生的模型要么因为局内点太少而被舍弃，要么因为比现有的模型更好而被选用。

步骤：

  1. 任意选择两个点组成直线，计算所有点到该直线的距离，如果小于某个阈值，那么归为内点
  2. 内点个数大于一定数目，采用该模型；否则继续步骤1，直到达到迭代次数。
    这里没有进行评估模型的步骤，直接根据内点的个数来选择模型。
    相关公式：
  3. 点$({x_0},{y_0})$到直线$Ax+By+C=0$的距离

$$ d= \left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|$$

  1. 已知两点$({x_1},{y_1})$，$({x_2},{y_2})$，可以得到直线的一般式方程$Ax+By+C=0$，其中
    $$ A=y_2-y_1 $$
    $$ B=x_1-x_2 $$
    $$ C=x_2y_1-x_1y_2 $$

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
# -*- coding:utf-8 -*-
import random
import math
import numpy as np
import matplotlib.pyplot as plt
# 生成的直线参数
k = 2.5;
b = 100;
dataN = 100;
noiseN = 5;
N = dataN + noiseN;
x = [];
y = [];
for i in range(dataN):
    x.append(i);
    y.append(i * k + b + random.uniform(-50, 20));
# 加入随机点
for i in range(noiseN):
    x.append(random.uniform(0, 200));
    y.append(random.uniform(0, 200));
axes = plt.subplot(211)
axes.scatter(x, y, s=20, c='red')
plt.ylabel('Least Squares Fitting')
axes = plt.subplot(212)
axes.scatter(x, y, s=20, c='red')
plt.ylabel('RANSAC')
# 最小二乘拟合
sumx = 0;
sumy = 0;
sumx2 = 0;
sumxy = 0;
for i in range(N):
    sumx += x[i];
    sumy += y[i];
    sumx2 += x[i] * x[i];
    sumxy += x[i] * y[i];
ls_k = (sumx * sumy - N * sumxy) / (sumx * sumx - N * sumx2);
ls_b = (sumx * sumxy - sumy * sumx2) / (sumx * sumx - N * sumx2);
ls_diff = []
for i in range(dataN):
    y1 = k * x[i] + b
    y2 = ls_k * x[i] + ls_b
    ls_diff.append(y2 - y1)
ls_diff_abs = [abs(x) for x in ls_diff]
ls_ava_err = sum(ls_diff_abs) / len(ls_diff_abs)
ls_std_err = np.std(ls_diff);
ls_x = [0, N];
ls_y = [ls_b, ls_k * N + ls_b];
plt.subplot(211)
plt.plot(ls_x, ls_y, linewidth=3);
plt.text(0, 0, 'ava:%f std:%f' % (ls_ava_err, ls_std_err))
# 随机一致估计拟合
dis_threshold = 30.0;
ransac_iters = 50;
class Point(object):
    X = 0
    Y = 0
    def __init__(self, x, y):
        self.X = x
        self.Y = y
# ax+by+c
class Line(object):
    a = 0;
    b = 0;
    c = 0;
    def __init__(self, p1, p2):
        self.a = p2.Y - p1.Y
        self.b = p1.X - p2.X
        self.c = p2.X * p1.Y - p1.X * p2.Y
    def distance(self, p):
        d = abs((self.a * p.X + self.b * p.Y + self.c) / math.sqrt(self.a * self.a + self.b * self.b))
        return d
    def gety(self, x):
        if (abs(self.b) < 1e-6):
            return 0
        else:
            return (self.a * x + self.c) / self.b * (-1.0)
best_line = None
best_count = 0
list = range(N)
best_point_x = []
best_point_y = []
for i in range(ransac_iters):
    idx = random.sample(list, 5)
    p1 = Point(x[idx[0]], y[idx[0]])
    p2 = Point(x[idx[1]], y[idx[1]])
    line = Line(p1, p2);
    count = 0;
    best_point_x.clear()
    best_point_y.clear()
    for j in range(N):
        p = Point(x[j], y[j])
        dis = line.distance(p)
        if (dis < dis_threshold):
            count = count + 1
            best_point_x.append(x[j])
            best_point_y.append(y[j])
        if (count > best_count):
            best_count = count
            best_line = line
if (best_line != None):
    ransac_x = [0, N];
    ransac_y = [best_line.gety(0), best_line.gety(N)]
    plt.subplot(212)
    plt.plot(ransac_x, ransac_y, linewidth=3)
    ransac_diff = []
    for i in range(dataN):
        y1 = k * x[i] + b
        y2 = best_line.gety(x[i])
        ransac_diff.append(y2 - y1)
    ransac_diff_abs = [abs(x) for x in ransac_diff]
    ransac_ava_err = sum(ransac_diff_abs) / len(ransac_diff_abs)
    ransac_std_err = np.std(ransac_diff);
    plt.text(0, 0, 'ava:%f std:%f' % (ransac_ava_err, ransac_std_err))
    axes.scatter(best_point_x, best_point_y, s=20, c='green')
plt.show()

结果

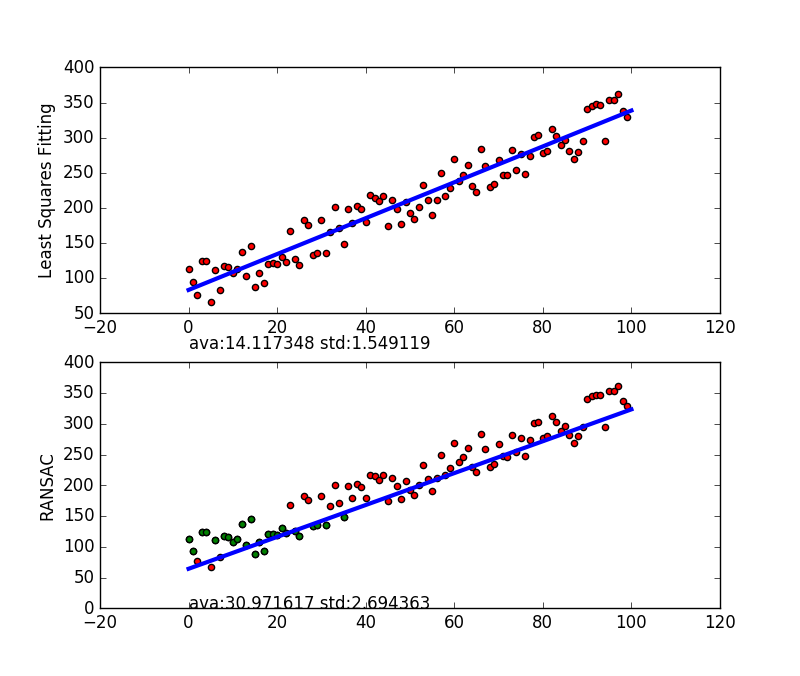
100正样本，无负样本

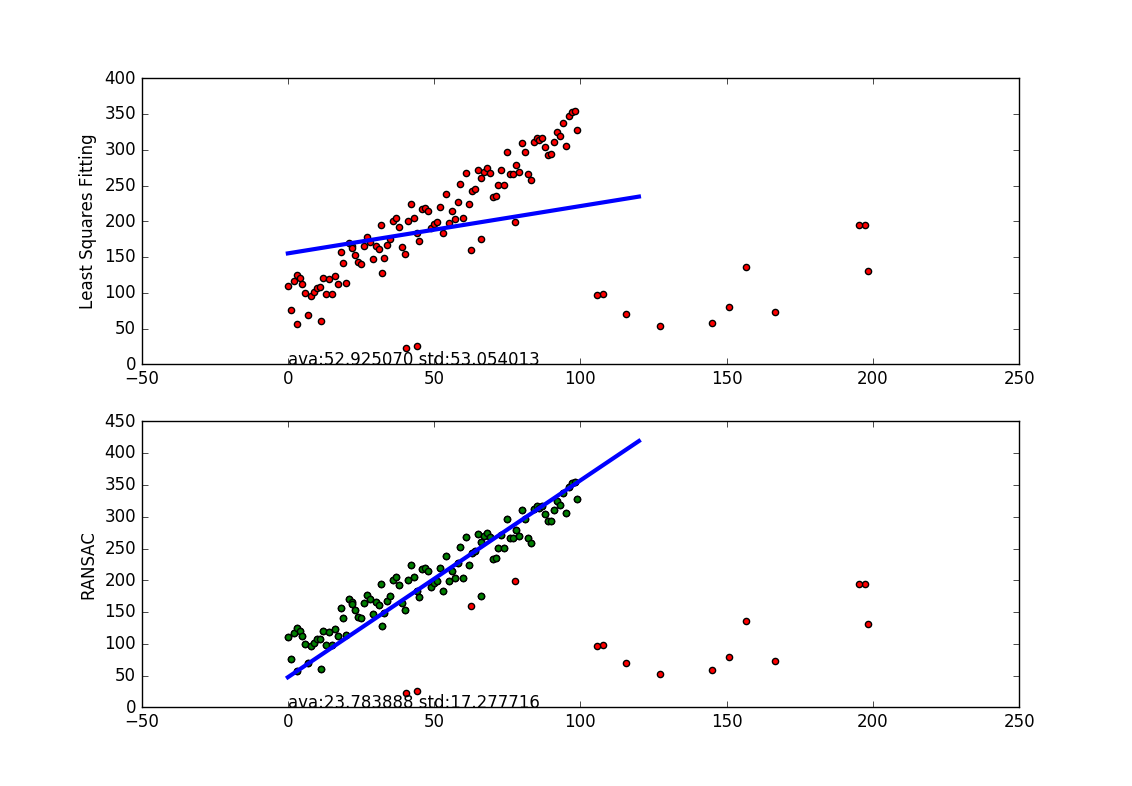
100正样本，20负样本

坚持原创技术分享，您的支持将鼓励我继续创作！