京东笔试题之幸运数字

题目

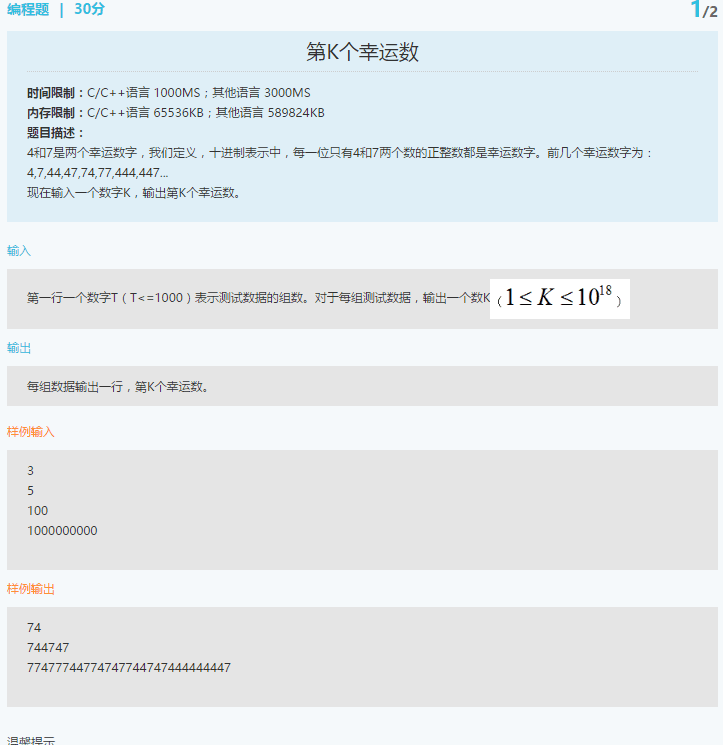
注意K的范围，程序中一定要用long long，用int达不到范围要求。
int ： -2147483648～2147483647
long long ： -9223372036854775808 ~ 9223372036854775807

解析

将4替换成0，7替换成1，那么幸运数字的排列如下：

1. 0
2. 1
3. 00
4. 01
5. 10
6. 11
7. 000
8. 001
9. 010
10. 011
11. 100
12. 101
13. 110
14. 100
    ……

下面介绍两种思路：

解法一

观察上表，发现规律如下：

$2^1$位数的所有顺序排列二进制
$2^2$位数的所有顺序排列二进制
$2^3$位数的所有顺序排列二进制
……
$2^n$位数的所有顺序排列二进制

所以我们可以先求得输入序号属于的n，再求出该值，然后打印该二进制即可。例如13，在属于n=3的组中，该组的第一个数字的序号是7，所以求得13-7=6，打印6的二进制，位是1输出”7”，是0输出”4”。

//这里没有读入用例个数T，直接输入n，输出第n个幸运数字

#include <iostream>

using namespace std;

int main()
{
	long long  n;
	
	while (cin >> n)
	{
		if (n <= 0LL)
			continue;

		long long power2 = 1;
		long long sum = 1;
		long long last = 0;
		long long bits_cnt = 0;

		for (int i = 0; i < n; ++i)
		{
			bits_cnt++;

			if (n >= sum && n < sum + power2 << 1)
			{
				last = n - sum;
				break;
			}

			power2 = power2 <<1;
			sum += power2;
		}

		for (int i = bits_cnt - 1; i >= 0; --i)
		{
			if (last & 1 << i)
				printf("7");
			else
				printf("4");
		}
		printf("\n");
	}
}

解法二

从表中可以获得第二个规律：

第1位的规律（从1开始）是：01010101…..
第2位的规律是（从1+2开始）：00110011…..
第3位的规律是（从1+2+4开始）：00001111…..
第n位的规律是（从1+2+4+…+$2^{n-1}$开始）：$
\begin{array}{c}
\underbrace{0\cdots 0}\\
\textrm{n}\\
\end{array}\begin{array}{c}
\underbrace{1\cdots 1}\\
\textrm{n}\\
\end{array}\cdots
$

…..

还以13举例,将13-1得12，这样变成序号从0开始，
第1位：
$12 \% 2^1=0 < \frac{2^1}{2}$，即该位在前半部分（0）,更新序号$12-2^1=10$作为下一位输入
第2位：
$10 \% 2^2=2 \geqslant \frac{2^2}{2}$，即该位在后半部分（1）,更新序号$10-2^2=6$作为下一位输入
第2位：
$6 \% 2^3=6 \geqslant \frac{2^3}{2}$即该位在后半部分（1）,序号$6<2^3$，算法停止。

逆序输出得到110，即“774”.

代码略。